Ä°lk olarak kimler tarafından keÅfedildiÄi bilinmese de, Mısırlılar’ın ve Yunanlılar’ın bu konu üzerinde yapmıŠoldukları bazı çalıÅmalar olduÄu görülmektedir. Öklid, milattan önce 300′lü yıllarda yazdıÄı “elementler” adlı tezinde “ekstrem ve önemli oranda bölmek” olarak altın oranı ifade etmiÅtir. Mısırlıların Keops Piramidinde, Leonardo da Vinci’nin “Ä°lahi Oran” adlı çalıÅmada sunduÄu resimlerde kullanıldıÄı bilinen "altın oran" , “Fibonacci Sayıları” olarak da bilinmektedir.
Orta ÇaĒın en ünlü matematikçisi olan Ä°talyan kökenli Leonardo Fibonacci, birbiri arasında ardıÅık iliÅki ve olaÄanüstü bir oran bulunduÄunu iddia ettiÄi sayıları keÅfetmiÅ ya da diÄer bir görüÅe göre de Hint-Arap medeniyetinden öÄrenmiÅ ve Avrupa'ya taÅımıÅtır. Evrendeki muhteÅem düzenle birebir örtüÅen bu sayıları keÅfetmesi nedeniyle, altın orana da adının ilk iki harfi olan “Fi” (Φ) sayısı denilmiÅtir.
Bir doÄru parçasının (AC) Altın Oran'a uygun biçimde iki parçaya bölünmesi gerektiÄinde, bu doÄru öyle bir noktadan (B) bölünmelidir ki; küçük parçanın (AB) büyük parçaya (BC) oranı, büyük parçanın (BC) bütün doÄruya (AC) oranına eÅit olsun.
BildiÄimiz gibi matematikte 3.14 sayısına karÅılık gelen ve bir dairenin çevresinin çapına bölünmesiyle elde edilen sayıya PÄ° (∏) sayısı denir. Aynı PÄ° sayısı gibi altın oran da matematikte 1.618 e eÅit olan sayıya denir ve Fi(φ) simgesiyle gösterilir ve ondalık sistemde yazılıÅı; 1,618033988749894...'tür.
Bu oranın kısaca gösterimi:  Åeklindedir.
Åeklindedir.
Altın Oran'ı tanımlamaya, bir kare çizerek baÅlayalım...

Åimdi, bu kareyi tam ortadan ikiye bölelim... Ä°ki eÅit dikdörtgen olacak Åekilde...

Dikdörtgenlerin ortak kenarının, karenin tabanını kestiÄi noktaya (C noktasına) pergelimizi koyalım.
Pergelimizi öyle açalım ki, çizeceÄimiz daire, karenin karÅı köÅesine deÄsin, yani dairemizin yarı çapı, bir dikdörtgenin köÅegeni olsun.
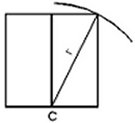
Sonra, karenin tabanını, çizdiÄimiz daireyle kesiÅene kadar uzatalım.
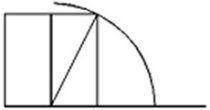
Yeni çıkan Åekli bir dikdörtgene tamamladıÄımızda, karenin yanında yeni bir dikdörtgen elde etmiÅ olacaÄız.
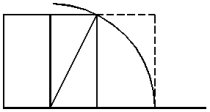
Ä°Åte bu yeni dikdörtgenin taban uzunluÄunun (B) karenin taban uzunluÄuna oranı Altın Oran'dır. Karenin taban uzunluÄunun (A) büyük dikdörtgenin taban uzunluÄuna (C) oranı da Altın Oran'dır. A / B = 1.6180339 = Altın Oran C / A = 1.6180339 = Altın Oran

Elde ettiÄimiz bu dikdörtgen ise, bir Altın dikdörtgendir. Çünkü uzun kenarının, kısa kenarına oranı 1.618 dir, yani Altın Oran'dır.
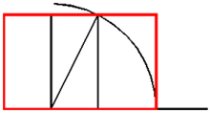
Artık bu dikdörtgenden her defasında bir kare çıkardıÄımızda elimizde kalan, hep bir "Altın Dikdörtgen" olacaktır.

Ä°çinden defalarca kareler çıkardıÄımız bu Altın Dikdörtgen'in karelerinin kenar uzunluklarını yarıçap alan bir çember parçasını her karenin içine çizersek, bir "Altın Spiral" elde ederiz. Altın Spiral, birçok canlı ve cansız varlıÄın biçimini ve yapı taÅını oluÅturur. Buna örnek olarak AyçiçeÄi bitkisini gösterebiliriz. AyçiçeÄinin çekirdekleri altın oranı takip eden bir spiral oluÅturacak Åekilde dizilirler. Altın oran, sadece dörtgenlerde deÄil, üçgen, beÅgen ve altıgenlerde de geçerlidir.

Bu karelerin kenar uzunlukları sırasıyla Fibonacci sayılarını verir.
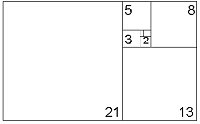
Fibonacci dizisi, her sayının kendinden öncekiyle toplanması sonucu oluÅan bir sayı dizisidir. Bu Åekilde devam eden bu dizide sayılar birbirleriyle oranlandıÄında "altın oran" ortaya çıkar, yani bir sayı kendisinden önceki sayıya böluÌndüÄuÌnde altın orana gittikçe yaklaÅan bir dizi elde edilir.
Fibonacci sayıları : 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765... Åeklinde devam eder. Bu ardıÅık sayılar dizisi ile Altın Oran arasında ilginç bir iliÅki vardır:
Fibonacci sayıları, kendisinden önceki iki sayının toplamı ile devam etmektedir. ÖrneÄin 13 sayısı kendisinden önceki iki sayının (5+8) toplamını göstermektedir.
“Ä°yi de, peki bu sayıların altın oran ile baÄlantısı nedir?” sorusu aklımıza gelebilir, onu da Åöyle açıklayalım:
Bir Fibonacci sayısının ile kendinden önceki sayıya böluÌmuÌ ile elde edilen sonuç, 1,618'dir. ÖrneÄin; 6765 / 4181 = 1,618… sonucunu vermektedir. Bu durum, 89!dan daha kuÌçuÌk olan Fibonacci sayıları için 0,01 gibi kuÌçuÌk bir farklılıkla ortaya çıksa da, buÌyuÌk sayıların tamamında sonuç aynıdır. Yani dizideki ardıÅık iki sayının oranı, sayılar büyüdükçe Altın Oran'a yani 1.618'e yaklaÅır, 89/55 ve sonrasında ise 1.618..'de sabitlenir.
Altın oranın karÅılık geldiÄi 1,618 sayısının matematikteki en ÅaÅırtıcı yanı, tersinin bir eksiÄine; karesinin ise bir fazlasına eÅit olmasıdır. Bu yönuÌyle altın oran (Φ) evrende eÅi benzeri olmayan, bu özelliÄe sahip tek sayıdır. Bu kuralı biraz açarsak, Åunları söyleyebiliriz:
Bir sayının tersi, 1'in o sayıya böluÌnmesi ile elde edilen sonuçtur. ÖrneÄin 2‘nin tersi 1/2=0,5‘tir.
Altın oranın tersi ise, 1 / 1,618 = 0,618‘dir. Yani altın oranın tersi, kendisinin 1 eksiÄine eÅittir.
Aynı Åekilde altın oranın karesi (1,618)2 = 2,618‘e, yani kendisinin bir fazlasına eÅittir.
Bu, ÅaÅkınlık verecek bir durumdur ve bu özellikte baÅka bir sayı yoktur!
Altın oran veya Fibonacci sayıları, buguÌne kadar insan yapımı birçok çalıÅmada kullanılmıÅtır. Bunun yanında doÄada var olan nesnelerin birçoÄunda altın oranın var olduÄu keÅfedilmiÅtir.
Mesela Ä°NSAN VÜCUDU....
(ANCAK DÄ°KKAT; elimize bir cetvel alıp ölçmeye kalkmayalım... Zira bu ölçümler bilim adamlarınca kabul edilen ideale en yakın vücut ölçüleri içindir. Ölçüler bu orana ne kadar yakın ise o kadar ideal kabul edilmiÅtir. )
BÄ°TKÄ°LER...
VE HAYVANLAR....